 |
| El comportamiento de los gases puede predecirse mediante la ecuación de los gases ideales a presiones bajas. Imagen de allmacwallpaper |
En este artículo describiremos el modelo de gas ideal, la ley de gas ideal y la validez de la ley de gases ideales para poder aplicar estos conceptos, por ejemplo, al aplicar la primera ley de la termodinámica.
Tabla de contenidos
Definición del modelo de gas ideal
 |
| El modelo de gas ideal permite idealizar un gas real para poder estudiar su comportamiento. Image de taful |
Los modelos matemáticos son utilizados para describir diferentes fenómenos que ocurren en la naturaleza mediante ecuaciones, gráficos y herramientas aritméticas, así como, tabulaciones de experiencias de laboratorio. El modelo de gas ideal es uno de los más utilizados en el estudio de la termodinámica y lo definiremos a continuación:
El modelo de gas ideal es aquel modelo matemático que se utiliza para describir y predecir el comportamiento de los gases.
Esta sencilla descripción se basa en el estudio del confinamiento de muestras de gas. En estos estudios, en un mol de varios gases en volúmenes de contención iguales (manteniendo dichas muestras a la misma temperatura), se observó que bajo estas condiciones la temperatura de los gases fue casi la misma. Además, se observó que si los gases tenían densidades bajas, esa diferencia de temperatura era casi nula. Bajo estas experiencias, se concluyó que dichos gases obedecen a una ley que se conoce como ley de los gases ideales.
Asimismo, se comprobó que los gases que obedecen el modelo de gas ideal, también obedecen a la ecuación que relaciona la energía interna de dichos gases con la temperatura, y es la ecuación conocida como calor específico.
Basamento del modelo de gas ideal
El modelo de gas ideal se basa en varios supuestos, los cuales veremos a continuación:- Las propiedades termodinámicas (P, V y T) se rigen por la ley de gases ideales.
- La energía interna se expresa en función de la temperatura.
- La masa molar de un gas ideal es igual a la masa molar de la sustancia real.
- Los calores específicos (Cv y Cp) son constantes.
También se han realizado otros supuestos para definir el modelo de gas ideal, como es el caso de los supuestos macroscópicos:
- Las moléculas de gas son esféricas de un tamaño muy reducido y duras.
- Entre las moléculas de gas, solo hay fuerzas que determinan las colisiones entre ellas.
- El movimiento de las moléculas de gas es sin fricción y las colisiones entre dichas moléculas son del tipo elásticas.
- La distancia promedio entre las moléculas de gas es mucho mayor al tamaño de una molécula de gas.
- El movimiento de las moléculas de gas es aleatorio.
- Las moléculas de gas no experimentan entre sí fuerzas atractivas o repulsivas.
Definido el modelo de gas ideal y los supuestos tomados para llegar a su conclusión, a continuación vamos a describir las leyes y ecuaciones que rigen al modelo de gas ideal.
Definición de gas ideal
 |
| Desviaciones del comportamiento del gas real frente al gas ideal. Imagen de slideshare |
El comportamiento de un gas es algo complicado, ya que se encuentra conformado por millones de moléculas que pueden colisionar entre sí. Al ser tan complejo describir el comportamiento de un gas real, se creó el concepto de gas ideal, el cual trata de describir el comportamiento de los gases en condiciones ideales.
Podemos decir entonces, que un gas ideal es aquel gas compuesto por moléculas y que sigue las siguientes reglas:
- Las moléculas del gas no se atraen ni se repelen entre sí, siendo la única interacción entre ellas las colisiones entre sí y con las paredes del recipiente que contiene al gas.
- Las moléculas del gas por sí mismas no ocupan ningún volumen, es decir, el gas tiene volumen ya que sus moléculas se expanden a través de todo el espacio que las contiene, pero las moléculas en sí no tienen volumen, ya que son partículas puntuales.
Como podemos notar, es un estado realmente ideal y que no describe el comportamiento de un gas en la realidad. Sin embargo, muchos gases tienden a comportarse de esta manera bajo ciertas condiciones, como por ejemplo, presiones muy bajas (cercanas a la presión atmosférica) y temperaturas muy similares a la temperatura ambiente, por lo cual, es posible estudiar estos gases bajo la ley de los gases ideales.
Adicionalmente, hay que tener en cuenta que los gases de gran volumen o los gases a presiones muy altas, presentan grandes desviaciones sobre la ley de gases ideales. Con todo esto en cuenta, podemos definir a un gas ideal teórico de la siguiente manera:
Un gas ideal es aquel gas compuesto por un conjunto de partículas puntuales, las cuales tienen un comportamiento aleatorio y no interactúan entre sí.
Ley de gas ideal
 |
| Deducción de la ecuación de gas ideal. Imagen de slideshare |
La ley de gas ideal, según la termodinámica clásica, es una fórmula que permite relacionar propiedades de los gases, como la presión, el volumen que ocupa el gas y su temperatura. Esta fórmula es muy simple y la podemos expresar de la siguiente manera:
Donde:
- P: Presión a la cual se encuentra el gas.
- V: Volumen que ocupa el gas.
- n: Número de moles del gas (cantidad de sustancia del gas).
- R: Constante de los gases (8.314 JK-1mol-1 o 0.082 (L*atm)/(K*mol)).
- T: Temperatura a la cual se encuentra el gas.
En la naturaleza, los gases ideales no existen. Sin embargo, los gases reales pueden comportarse como ideales, siempre y cuando estos gases se encuentren a presiones bajas (en relación a la presión crítica) y a temperaturas elevadas (en relación a la temperatura crítica).
Podemos observar que la ley de gas ideal es la misma ley general de los gases, solo que el factor de compresibilidad (factor que mide la desviación del comportamiento de un gas respecto al comportamiento de un gas ideal) de dicho gas es igual a 1.
Energía interna del gas ideal
La otra ecuación que forma parte del modelo de gas ideal es la de la energía interna del gas. Para ello, primeramente, debemos tomar en cuenta el calor específico.A volumen constante, el calor específico del gas ideal es expresado por:
Mientras que a presión constante, el calor específico se expresa de la siguiente manera:
Destacando que la entalpía de un gas es:
Entonces, podemos expresar a la energía interna del gas ideal en función de la temperatura a la cual se encuentra, de la siguiente manera:
Donde:
- U: Energía interna del sistema.
- Cv: Calor específico a volumen constante.
- n: Número de moles del gas.
- R: Constante de los gases. T: Temperatura a la cual se encuentra el gas.

Modelo de gas ideal by Ing. Bulmaro Noguera is licensed under a Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional License

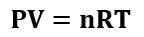

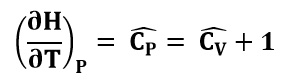












0 Comentarios