La extracción líquido-líquido es una técnica de separación de compuestos químicos de un solvente A a un solvente B. En otras palabras, la extracción líquido-líquido es un intercambio de ciertos compuestos entre dos disolventes diferentes que son inmiscibles o parcialmente miscibles entre sí. Este tipo de separación es muy efectiva y es comúnmente utilizada para lavar fases orgánicas, para eliminar compuestos inorgánicos, o para protonar o desprotonar bases o ácidos para hacerlos solubles en soluciones acuosas.
 |
| Equipos para extracción líquido-líquido. Imagen de eringenierie |
En este artículo describiremos los fundamentos de la extracción líquido-líquido y la representación gráfica de sistemas ternarios con ejemplos.
Tabla de contenidos
- ✔Extracción líquido-líquido: Definición y descripción
- ✔Requisitos del disolvente para una extracción líquido-líquido
- ✔Equilibrios de extracción líquido-líquido
- ✔Representación gráfica de sistemas ternarios para extracción líquido-líquido
- ✔Caso 1: Triángulo equilátero
- ✔Caso 2: Triángulo rectángulo
- ✔Caso 3: Diagrama de distribución de equilibrio
- ✔Caso 4: Diagrama de selectividad
- ✔Caso 5: Diagrama de concentración-contenido en disolvente
- ✔Interpolación de rectas de reparto en extracción líquido-líquido
Extracción líquido-líquido: Definición y descripción
 |
| Planta donde se realiza extracción líquido-líquido. Imagen de technoforce |
La extracción líquido-líquido es la separación de los constituyentes de una disolución líquida, mediante el contacto con otra disolución inmiscible que disuelve preferentemente a uno de los constituyentes de la disolución original, dando como resultado la aparición de dos capas líquidas inmiscibles de diferentes densidades. Es un proceso fundamental en la industria farmacéutica y química para separar productos entre sí.
En una extracción o separación líquido-líquido, la disolución a tratar es conocida como “alimentación”, mientras que el líquido que se pone en contacto con esta disolución se conoce como “disolvente”. Una vez que ocurre el contacto entre la alimentación y el disolvente, se obtienen dos fases líquidas, conocidas como:
- Extracto: Fase líquida rica en solvente.
- Refinado: Fase líquida pobre en disolvente.
La idea principal de la extracción líquido-líquido es dividir la disolución original en producto extraído y producto refinado. Para ello, es fundamental la extracción del disolvente añadido a la disolución, siendo importante que la recuperación del disolvente pueda efectuarse de forma sencilla y económica. Por lo general, esta recuperación se realiza mediante destilación, evaporación o salinificación.
Podemos decir entonces que la extracción líquido-líquido, consta de tres pasos principales:
- Contacto de la alimentación con el disolvente.
- Separación de las fases líquidas formadas (extracto y refinado).
- Recuperación de disolvente.
A estos tres pasos se les conoce como estadío, etapa o unidad de extracción, y reciben el nombre de ideal o teórico, cuando el contacto entre la disolución líquida y el disolvente ha sido suficiente para que las fases líquidas separadas tengan las concentraciones correspondientes a condiciones de equilibrio.
Los diferentes métodos de extracción, difieren en la forma de efectuar la mezcla con el disolvente y la separación de las fases formadas en cada uno de los estadíos o etapas.
Requisitos del disolvente para una extracción líquido-líquido
Para realizar una extracción líquido-líquido exitosa, el disolvente debe presentar las siguientes características:
- Máxima solubilidad del producto en el disolvente.
- Mínima solubilidad del disolvente en el refinado.
- Mínima solubilidad de la alimentación en el disolvente.
- Permitir una separación rápida de fases.
- Permitir una separación fácil del producto, a partir del extracto/disolvente.
Equilibrios de extracción líquido-líquido
Limitaremos nuestro estudio, al caso de la separación de dos constituyentes de una mezcla líquida a la que se le añade un componente, que es capaz de disolver de manera selectiva a uno de los constituyentes de la mezcla líquida original.
Denominaremos coeficiente de distribución o coeficiente de reparto de un componente i entre las dos fases líquidas separadas extracto (E) y refinado (R), a la relación entre las concentraciones que alcanza dicho componente en ambas fases en equilibrio. Podemos representarlo matemáticamente de la siguiente manera:
Este coeficiente dependerá directamente del disolvente empleado, de la composición de la mezcla y de la temperatura de operación. En el caso más simple, el soluto contenido en la disolución original se distribuye entre las dos fases líquidas inmiscibles, pero en la gran mayoría de los casos los dos disolventes son parcialmente miscibles entre sí y la concentración del soluto influye en la solubilidad mutua de ambos componentes.
Cabe destacar, que el conocimiento de los datos de equilibrio correspondientes a los tres sistemas binarios que constituyen el sistema ternario, es insuficiente para predecir el comportamiento del coeficiente. Los datos de equilibrio han de determinarse experimentalmente y deben representarse en gráficas adecuadas.
Representación gráfica de sistemas ternarios para extracción líquido-líquido
Seguidamente, describiremos la representación gráfica de sistemas ternarios para extracción líquido-líquido y sus diferentes casos.
Caso 1: Triángulo equilátero
Cuando se trabaja en este tipo de diagrama, cada uno de los vértices del triángulo representa a los componentes puros. Sobre cada lado se representan las mezclas binarias de los componentes que se encuentran en los vértices correspondientes a ese lado, y cualquier punto exterior representa una mezcla ternaria, de modo, que la cantidad relativa de cada componente en la mezcla es proporcional a la distancia al lado opuesto (a, b, c en la siguiente figura).
 |
| Ubicación de puntos en diagramas triangulares |
Teniendo en cuenta que la suma de estas distancias es igual a la altura del triángulo, el cociente de cada una por la suma representará a la cantidad relativa del componente respecto a la mezcla.
Los segmentos a, b y c son proporcionales a los segmentos a’, b’ y c’ (paralelos a los lados del triángulo) y su suma es igual al lado del triángulo. Con el mismo fin, se pueden tomar las medidas de los segmentos a’, b’ y c’ con el lado como unidad de longitud.
Las unidades de concentración de este diagrama suelen ser las fracciones en peso o fracciones molares. En cualquier caso, la suma de concentraciones ha de ser constante para todas las composiciones. Las siguientes propiedades, hacen a este diagrama particularmente útil para los cálculos de extracción:
- Las mezclas cuyas composiciones corresponden a los puntos sobre una recta paralela a un lado, tienen concentración constante del componente situado en el vértice opuesto
- Los puntos del segmento que unen un vértice con un punto del lado opuesto, representan mezclas de una misma relación constante entre las concentraciones de los componentes situados en los otros dos vértices.
- Cuando se añade una mezcla representada por P1, un componente puro, u otra mezcla representada por P2, el punto P representativo de la composición final se encuentra en el segmento P1P2 que une los puntos representativos de las partes y determina dos segmentos P1P y P2P, inversamente proporcionales a las cantidades de cada parte (regla de la palanca).
A continuación, veremos un par de ejemplos para explicar gráficamente lo anteriormente descrito.
Ejemplo 1
 |
| Diagrama del ejemplo 1 |
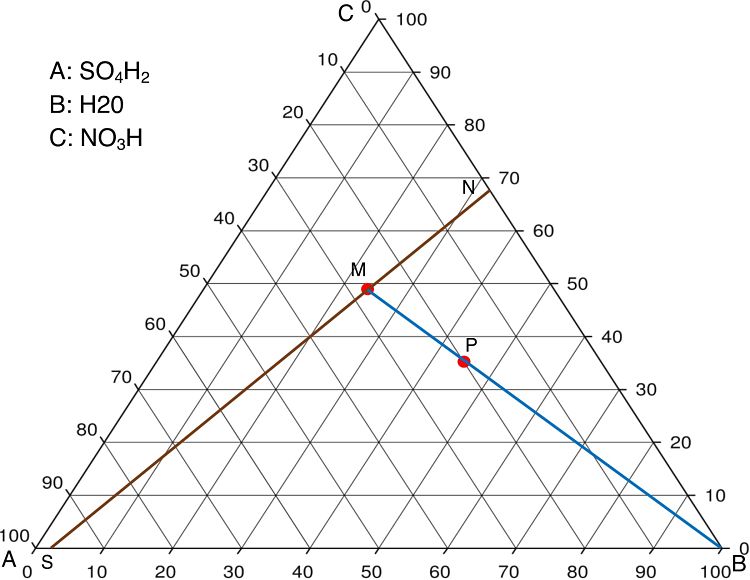
A partir del SO4H2 al 98% en peso, NO3H al 68% en peso y de agua, se ha de preparar 500 Kg de una disolución cuya composición en peso sea 35% de NO3H, 20% de SO4H2 y 45% de H2O. Empleando un diagrama triangular, calcular la cantidad necesaria de cada uno de los componentes.
Solución
Primeramente, fijamos sobre el diagrama triangular los puntos correspondientes a cada componente. Hemos nombrado “S” al punto del lado AB, “N” al punto del lado BC, “B” al vértice de agua pura y “P” al punto de la disolución a preparar. La intersección de las rectas BP y SN fija el punto “M” que corresponde a la mezcla S y N, de modo, que al añadirle B nos lleva al punto P.
Sobre el diagrama triangular se lee la composición de M que es 0,4865 con respecto al NO3H.
Para calcular las cantidades de M y B aplicamos la regla de la palanca al segmento MB, de la siguiente manera:
La relación queda así:
Por otra parte, como M + B = 500, sustituimos el valor de M, resultando:
B=140,3 Kg y M=359,7 Kg
Para calcular las cantidades de S y N aplicamos la regla de la palanca al segmento SN:
Teniendo en cuenta que:
Los valores de N y S serían:
S=102,4 Kg y N=257,3Kg
Ejemplo 2
1000 Kg de mezcla ácida de composición 30% en peso de SO4H2, 20 % en peso de NO3H y 50% de H20, se ha de modificar añadiéndose SO4H2 al 98 % y NO3H al 90 %, para dar una disolución cuya composición sea de 50% de SO4H2, 30 % de NO3H y 20 % de H2O. Empleando un diagrama triangular, calcular las cantidades que han de añadirse de los dos ácidos concentrados.
Solución
 |
| Diagrama del ejemplo 2 |
Al igual que en el ejercicio anterior, procedemos a graficar los puntos correspondientes: F para la alimentación, los puntos S y N, además del punto de mezcla P. Luego, se trazan las rectas y estaremos listos para aplicar la regla de la palanca:
Despejando, tenemos que:
De forma similar:
Despejando:
Además, sabemos que:
Resolviendo, tenemos los siguientes resultados:
S =1225 Kg
N = 775 Kg
Ahora, que ya tenemos idea de cómo graficar en este tipo de diagramas ternarios o triángulo de Gibbs, debemos aclarar que como principio fundamental de la extracción líquido-líquido, la adición de disolvente ha de generar la aparición de dos fases líquidas.
Si consideramos que el disolvente B es parcialmente miscible con uno de los constituyentes de la mezcla a separar, y totalmente miscible con el otro componente, en el vértice superior colocamos al componente C miscible con B y en el vértice inferior izquierdo colocamos al componente A parcialmente miscible con B.
Este tipo de sistemas formado por dos sistemas binarios completamente miscibles y un sistema binario parcialmente miscible, es el que se presenta con más frecuencia en la extracción líquido-líquido y se conoce como sistema 3,1 (3 componentes y 1 sistema binario parcialmente miscible).
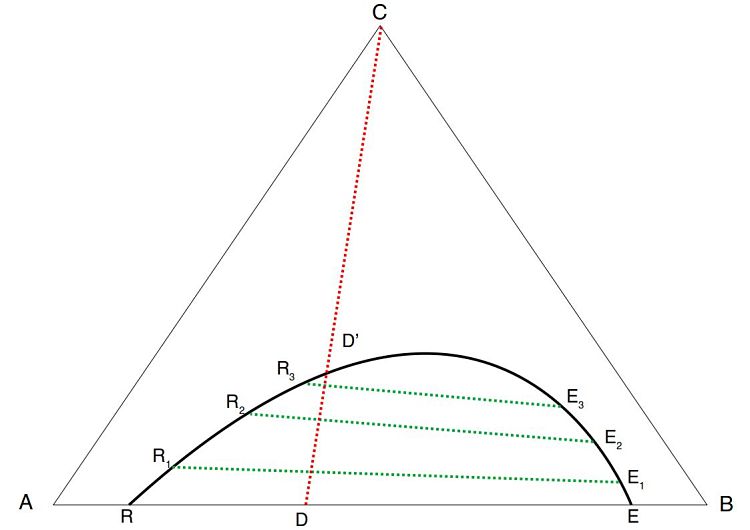
Tomando una mezcla de los componentes A y B, cuya composición global viene dada por el punto D (ver figura) en el equilibrio a una temperatura dada, la mezcla se separa en dos fases líquidas representadas por los puntos E y R, cuya concentración relativa depende del grado de miscibilidad de A con B, de modo, que si fueran completamente inmisicibles, las posiciones de estos puntos coincidirían con los vértices B y A y estarían tanto más cerca de ellos, como cuanto mayor sea su inmiscibilidad. La mezcla E rica en el componente A, estará saturada de componente B. La porción entre ambas fases líquidas vendrá dada por el cociente entre los segmentos DR/DE.
 |
| Distribución de fases líquidas en la extracción líquido-líquido |
Si a la mezcla global D le añadimos el componente C, este componente se distribuirá entre las dos fases líquidas formando disoluciones ternarias conjugadas (E1,R1; E2,R2; E3,R3; etc) e irá variando la proporción relativa de ambas fases a medida que se va añadiendo al componente C, hasta alcanzar al punto D’ en el que desaparece una de las fases líquidas y la mezcla deja de ser heterogénea.
Si partimos de varias mezclas globales de A y B (como podemos ver en la siguiente figura), se puede determinar para cada una de las mezclas binarias de partida, la cantidad necesaria de componente C’, F’, G’ y H’, etc, que determinan las curvas binodales o isotermas de saturación, de modo, que el área comprendida bajo esa curva corresponde a sistemas heterogéneos. Cualquier mezcla cuya composición global se encuentre dentro de esta zona se separará en dos fases conjugadas, cuyas composiciones se encuentran sobre la curva binodal. La recta que une los puntos de las fases conjugadas se denomina recta de reparto.
 |
| Curva binodal de diagrama ternario de extracción líquido-líquido |
La pendiente de las rectas de reparto, varía con las concentraciones y la naturaleza de la mezcla, pudiendo presentarse los tres casos indicados en la siguiente figura:
- Caso a: Fase E es más rica en C que fase R. La distribución del componente C está favorecida hacia la fase más rica de B.
- Caso b: La distribución de C no está favorecida hacia ninguna de las fases.
- Caso c: La distribución del componente C está favorecida hacia la fase más rica en A.
 |
| Diferentes casos de curva binodal |
Observando las rectas de reparto, notamos que al aumentar la cantidad del componente C, la composición de ambas fases se aproxima. En el punto P las dos disoluciones conjugadas tienen la misma composición, de modo, que las dos fases se transforman en una sola fase. A este punto, se le denomina punto crítico del sistema o punto de pliegue.
En las consideraciones anteriores, limitamos los casos a que un componente es completamente miscible con los otros dos, que a su vez son parcialmente miscibles entre sí (sistema 3,1). En los casos menos frecuentes, donde las mezclas A y B, así como A y C, son parcialmente miscibles, estaríamos ante sistemas 3,2 ( 3 componentes, 2 sistemas binarios). La representación gráfica la podemos ver a continuación:
 |
| Sistemas del tipo 3,2 |
Cuando las tres mezclas (AB, BC y CD) son parcialmente miscibles, nos encontramos con un sistema del tipo 3,3 (3 componentes, 3 sistemas binarios parcialmente miscibles). Su representación gráfica es la siguiente:
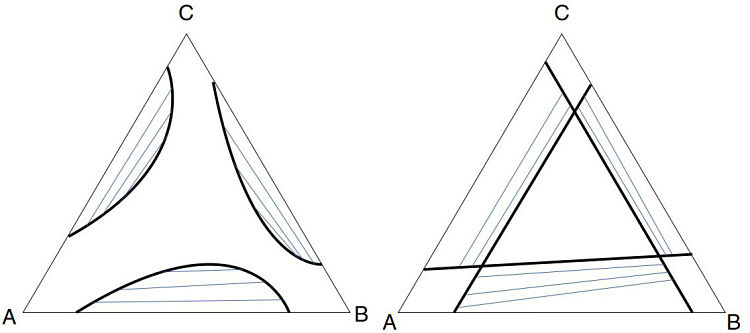 |
| Sistemas del tipo 3,3 |
Caso 2: Triángulo rectángulo
Este tipo de diagramas, representa en el eje de las abscisas a la concentración o fracción (molar o porcentaje en peso) del componente B y en el eje de las ordenadas la composición del componente C. Las propiedades fundamentales son análogas a la representación del diagrama de triángulo equilátero.
El diagrama de triángulo rectángulo cuenta con la ventaja (sobre los diagramas de triángulo equilátero) de que permite cambiar las escalas de los ejes coordenados. La analogía, con respecto al gráfico anterior, la podemos ver en la siguiente figura:
 |
| Analogía de diagrama de triángulo rectángulo con respecto al diagrama de triángulo equilatero |
Caso 3: Diagrama de distribución de equilibrio
Se trata de un diagrama del tipo rectangular, en el cual el eje de las abscisas representa la composición porcentual del soluto en el refinado, mientras que el eje de las ordenadas representa la composición porcentual del soluto en el extracto, tomando ambas composiciones de los extremos de las rectas de reparto. Su construcción se basa en los datos del diagrama triangular, como podemos ver en la siguiente figura:
 |
| Diagrama de distribución de equilibrio |
Este tipo de diagrama, indica directamente la distribución del soluto en el extracto y el refinado para todas las concentraciones. Resulta de gran utilidad para estudiar de modo comparativo el empleo de distintos disolventes en el proceso de extracción líquido-líquido.
Si el coeficiente de distribución XE/XR del componente C respecto al extracto y al refinado es mayor que la unidad, la curva se encuentra por encima de la diagonal, indicando que C se distribuye en mayor proporción en el extracto que en el refinado. Para una situación contraria, la curva se ubicaría por debajo de la diagonal.
Caso 4: Diagrama de selectividad
En estos diagramas se representa en el eje de las abscisas la composición del soluto en el refinado libre de disolvente, XR = C/(A+C) y en el eje de las ordenadas, se representa la composición del soluto en el extracto en equilibrio.
Se calcula así: XE = C/(A+C). Este tipo de diagrama es muy importante en la extracción líquido-líquido, ya que la selectividad es el factor más importante a considerar en la elección del disolvente.
Podemos definir a la selectividad por la expresión matemática:
Conociendo que el grado de selectividad va a variar con la concentración y simultáneamente es función de la temperatura, las curvas representativas correspondientes a este tipo de diagrama pueden tomar la forma que se muestra en la siguiente figura:
 |
| Diagrama de selectividad |
La “I” corresponde a la distribución del soluto en el disolvente selectivo, la “II” corresponde a la distribución del soluto en el disolvente menos selectivo, la “III” corresponde a la aparición de un azeótropo y la “IV” corresponde a un caso en donde la selectividad de A por C es mayor a la de B por C.
Caso 5: Diagrama de concentración-contenido en disolvente
En estos diagramas, las ordenadas representan la cantidad de disolvente del extracto y del refinado, y se expresan así:
Frente a la concentración del soluto, que podemos expresar de la siguiente manera:
Estas representaciones se expresan sobre una base libre de disolvente. Podemos observarlas en la siguiente figura comparativa con el diagrama triangular:
 |
| Diagrama de concentración-contenido |
Interpolación de rectas de reparto en extracción líquido-líquido
Para poder realizar cualquier tipo de cálculo de extracción líquido-líquido sobre cualquiera de los diagramas vistos anteriormente, se requiere disponer de un método que permita trazar rectas de reparto por cualquier punto de la curva binodal, para poder interpolar entre las curvas de reparto determinadas de manera experimental.
Para realizar la interpolación, nos vamos a referir a sistemas del tipo 3,1 por ser los más comunes en los cálculos de extracción líquido-líquido. Los principales métodos de interpolación de rectas de reparto son los siguientes:
Método de Alders
Este método es el más utilizado y conduce a los resultados más satisfactorios. Una vez que se han levantado la curva binodal y las rectas de reparto, gracias a los datos experimentales, se trazan rectas paralelas a los lados del triángulo desde los extremos de las rectas de reparto. La intersección de estas rectas paralelas fijan puntos de fases conjugadas que permiten trazar la línea ILMKH’L’M’ que lleva el nombre de línea conjugada. Esta línea corta la curva binodal en el punto de pliegue K (ver figura).
 |
| Método Alders para interpolar rectas de reparto en extracción líquido-líquido |
Una vez trazada la línea conjugada, es muy sencillo realizar la interpolación de las rectas de reparto. Si deseamos crear una recta de reparto que corresponda al punto S, se traza por ese punto una recta paralela al lado CB que cortará a la línea conjugada en el punto R. Desde ese punto se traza una paralela al lado AC que intercepta a la curva binodal en el punto S’ que es la fase conjugada de S, luego, se traza la recta SS’ que será la recta de reparto deseada.
Método de Sherwood
Se trata de una modificación del método de Alders. La diferencia radica en que las líneas paralelas a los lados AC y AB se realizan por dentro de la curva binodal, obteniéndose los puntos para trazar la línea conjugada ILMK, como podemos ver en la siguiente figura:
 |
| Método de Sherwood para interpolar rectas de reparto en extracción líquido-líquido |
Método de Tarasenkow y Paulsen
Este método se limita a los sistemas en los cuales las rectas de reparto tienen un punto común P de intersección sobre la prolongación de la base del triángulo, como podemos ver en la siguiente figura:
 |
| Método de Tarasenkow y Paulsen para interpolar rectas de reparto en extracción líquido-líquido |
Una vez fijado el punto P, la interpolación es simple e inmediata, sólo hay que seguir las líneas de reparto hasta identificar el punto P.
En un próximo artículo, describiremos los métodos de cálculo para los diferentes casos de extracción líquido-líquido. Como siempre, los invito a comentar la nota para establecer intercambio de ideas y complementar conceptos.

Fundamentos de extracción líquido-líquido by Ing. Bulmaro Noguera is licensed under a Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional License

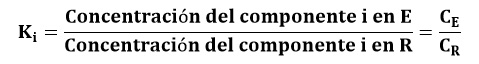






















2 Comentarios
Hola, para realizar la interpolación de las líneas de reparto en los diagramas de triángulo rectángulo, ¿se haría de la misma forma que con los triángulos equiláteros?
ResponderBorrarUn saludo
Gracias por tu comentario! La interpolación de líneas de reparto en un diagrama de triángulo rectángulo se utiliza para determinar la fracción molar de cada componente en cada fase líquida en una extracción líquido-líquido. Se puede realizar de varias maneras, pero un método común es el siguiente:
Borrar- Dibujar un diagrama de triángulo rectángulo con las concentraciones de los componentes en cada fase líquida en los ejes.
- Identificar la fracción molar inicial de cada componente en la fase líquida de alimentación.
- Utilizar las ecuaciones de equilibrio de la extracción líquido-líquido para calcular la fracción molar de cada componente en cada fase líquida después de la extracción.
- Conectar los puntos de fracción molar inicial y final de cada componente en cada fase líquida para formar una línea de reparto.
- Utilizar la interpolación para calcular la fracción molar de cada componente en cualquier punto de la línea de reparto.
Para realizar este procedimiento, es necesario tener información de los coeficientes de distribución de los componentes y las concentraciones iniciales. Saludos!