El factor de fricción de Darcy es un número adimensional (es decir, no presenta unidades de medida) que permite predecir las pérdidas de energía por fricción que presenta el interior de una tubería. Estas pérdidas se basan principalmente en la velocidad a la cual viaja el fluido dentro de la tubería, y la resistencia o rugosidad que se encuentra dentro de la tubería.
 |
| Las tuberías presentan una rugosidad que genera pérdidas de energía por fricción del flujo dentro de estas. Imagen de maxpixel |
Este factor de fricción de Darcy es fundamental para el desarrollo de una ecuación global de balance de energía que tome en cuenta la viscosidad del fluido que viaja a través de una tubería. Para ello, se utiliza la ecuación de Bernoulli generalizada que incluye un término que hace posible contabilizar las pérdidas de energía que resultan de la fricción en el interior de las tubería o ductos.
En este artículo definiremos el factor de fricción de Darcy, las principales consideraciones de pérdidas de energía por fricción y cómo realizar el cálculo de las pérdidas de energía por fricción.
Consideraciones sobre la pérdida de energía por fricción
Los fluidos reales poseen viscosidad, es por esta razón, que es inevitable la ocurrencia de pérdidas de energía por fricción en el flujo que viaja a través de las tuberías o ductos. Estas pérdidas de energía son designadas como hL y representan la energía mecánica que se transforma en calor. Si se supone que todo el calor generado por fricción se absorbe por el fluido, se puede expresar de la siguiente manera, tomando en consideración las pérdidas de energía:
La expresión anterior representa el calor total absorbido por el fluido. Considerando además que la energía interna de una unidad de masa de fluido dentro del volumen de control sólo puede cambiar mediante intercambio de calor, compresión y expansión con los alrededores, además de tomar en cuenta a la primera ley de la termodinámica, podemos expresar la variación de la energía interna de la siguiente manera:
Si se nota además, que:
Sustituyendo podemos llegar a la siguiente ecuación:
Esta ecuación es conocida como Bernoulli generalizada o ecuación de ingeniería. Podemos notar que toma en cuenta a las pérdidas de energía totales que ocurren en el volumen de control, incluyendo las pérdidas de tuberías y de accesorios, más las pérdidas de los equipos como bombas, turbinas, compresores, entre otros.
Cálculo de las pérdidas de energía por fricción
 |
| Rugosidad de una tubería. Imagen de lifeder |
Mediante estudios experimentales se ha comprobado que las pérdidas de cabezal en tuberías rectas y cilíndricas son directamente proporcionales al cabezal de velocidad y a la longitud de la tubería e inversamente proporcionales al diámetro de la tubería. Para lograr el cálculo de las pérdidas de energía, Darcy y otros investigadores propusieron la siguiente ecuación:
Donde:
- fD: Factor de fricción de Darcy
- L: Longitud de la tubería
- v: Velocidad del fluido
- g: Aceleración de gravedad
- D: Diámetro de la tubería
Esta ecuación se conoce como Darcy-Weisbach y es básica para el cálculo de pérdidas de cabezal o de energía, causadas por fricción del flujo completamente desarrollado (no por los accesorios) en tuberías rectas y largas de diámetro constante que corren llenas de líquido en condiciones isotérmicas. Para flujo compresible, la ecuación anterior se aplica sólo a una longitud diferencial de ducto (dL), a través de la cual, se considera que la densidad de dicho flujo es constante.
En tuberías curvadas, las pérdidas de energía son causadas por el efecto combinado de la separación de la capa límite, la fricción de las paredes y el flujo secundario. El primer y el tercer efecto no son tomados en cuenta por la ecuación antes descrita. El flujo secundario circula en forma de espiral, perpendicular a la dirección axial y superpuesto a la corriente de flujo.
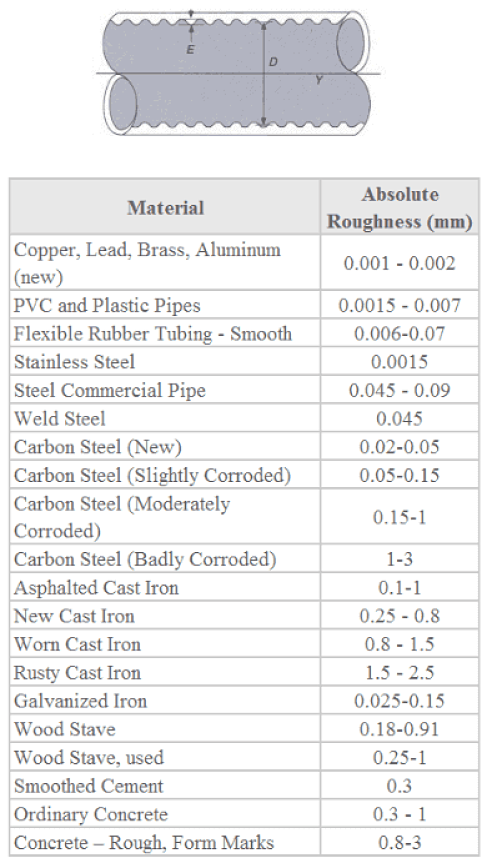 |
| Tabla de rugosidad absoluta de algunos tipos de tubería. Imagen de thermalengineering |
El factor de fricción de Darcy depende primeramente de la rugosidad interior de la tubería. Además, también va a depender de la velocidad promedio del flujo, del diámetro de la tubería y de la viscosidad del fluido. La rugosidad absoluta, se designa con la letra ε y representa las condiciones de la superficie interior de la tubería y de las proyecciones desde la pared de la tubería. Esta rugosidad absoluta puede encontrarse tabulada en los textos de fenómenos de transporte y dinámica de fluidos, y generalmente, es reportada por los fabricantes de las tuberías.
Cálculo del factor de fricción de Darcy
 |
| Diagrama de Moody. Imagen de thermalengineering |
Para el cálculo del factor de fricción de Darcy, generalmente se utiliza la gráfica de Moody. En dicha gráfica se puede ver al factor de fricción de Darcy como una función del número de Reynolds y la rugosidad relativa ε/D, siendo D el diámetro interno de la tubería.
Zona de flujo laminar
En esta zona se encuentra el flujo con un número de Reynolds (Re) menor a 2000, donde el factor de fricción de Darcy (fD) es completamente independiente de la rugosidad. La ecuación correspondiente a este comportamiento es la siguiente:
Zona crítica
Aquí, podemos encontrar fluido con un número de Reynolds (Re) ubicado en un rango que va desde los 2000 hasta los 4000. El comportamiento en esta zona es indefinido, dependiendo del comportamiento de factores externos, como cambios bruscos de diámetro de tubería, obstrucciones, etc.
Zona de transición
En esta zona, el factor de fricción de Darcy depende tanto del Re como de la rugosidad relativa. Para este rango intermedio existe una correlación (Colebrook) bastante aproximada, dada por la expresión:
Estas curvas son asintóticas en un extremo, a la curva correspondiente a tubos lisos, y en el otro extremo, a las líneas horizontales de la zona de tubos rugosos.
Zona de tubos rugosos
Aquí, la turbulencia es completa y el factor de fricción de Darcy es independiente del número de Reynolds. En este caso, el factor de fricción de Darcy se puede expresar mediante la ecuación de Von Karman:
También, puede observarse en la gráfica de Moody una curva designada por tubos lisos, para los que la ecuación es:
Esta ecuación se puede aplicar a cualquier tubería, siempre y cuando δ>1.7ε, siendo δ el espesor de la subcapa laminar. Cuando prevalece esta condición el flujo se conoce como “flujo liso”. Se ha encontrado esta ecuación confiable para tubos lisos y números de Reynolds superiores a 4000.
Conclusión
Podemos concluir que el factor de fricción de Darcy es un número o parámetro adimensional, comúnmente utilizado en los fenómenos de transporte y dinámica de fluidos, que permite estimar las pérdidas de energía por fricción en un ducto o una tubería, y que por lo general, puede estimarse utilizando el diagrama de Moody. Este factor de fricción de Darcy depende directamente del número de Reynolds del flujo y la rugosidad interna de la tubería.

El factor de fricción de Darcy y las pérdidas de energía por fricción by Ing. Bulmaro Noguera is licensed under a Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional License




















0 Comentarios